東大数学は得意な人と苦手な人で差がつきやすい科目です。
苦手な人は苦手なりに数学で差をつけられないようにし、得意な人は多く得点したいところですね。
- 知ってるだけで1点でも多く得点できる東大数学の傾向・対策
- 東大数学を攻略する上で最大効率な勉強方法
- 文系理系レベル別のオススメ参考書ルート
を紹介します。

KENTEN
東大数学の攻略が一番差がつくため、数学対策が合否を分けるといっても過言ではありません!
理Ⅰに現役合格した私が実践した攻略方法を教えます。
- 東大受験生で数学対策を考えている
- 東大数学の傾向と対策を知りたい
- 東大数学のオススメ参考書を知りたい
- 東大数学で1点でも多く取りたい
見たい場所に飛べる目次
東大数学の概要
理系では2次試験440点の3割を占める
2次試験の440点の内訳は、下記の科目と配点です。
| 科目 | 文系 | 理系 |
|---|---|---|
| 外国語 | 120 | 120 |
| 国語 | 120 | 80 |
| 数学 | 80 | 120 |
| 理科 | – | 120 |
| 社会 | 120 | – |
| 合計 | 440 | 440 |
理系においては数学の対策が合否を分けることになります。
2次試験の配点の3割近くを占める科目だからです。
文系においても配点こそ少ないものの、数学でしっかり得点できると他の科目がグッと楽になります。
出題形式・試験時間・配点
| 文系・理系 | 大問数 | 試験時間 | 配点 |
|---|---|---|---|
| 文系 | 4 | 100分 | 80点 |
| 理系 | 6 | 150分 | 120点 |
問題はすべて記述式です。
解答用紙も大問ごとに区切られたスペースがあるだけで、小問ごとの区切り線がないのが特徴的です。
配点の内訳は非公開ですが、各大問20点と考えられます。
出題範囲
- 文系は数学ⅠA・ⅡBから出題されます。(ただし数学Bは数列・ベクトル)
- 理系は文系範囲+Ⅲの範囲
東大数学の特徴
東大数学の難易度は高めです。
思考力と計算力が問われるからです。
思考力・実験力が必要
問題の初見では解法が思いつかないことがよくあります。
解を見つけるためには、手を使いながら進めていく作業が必要です。
計算力が必要
東大数学では解法は難しくなくても、複雑な計算が必要な問題が頻出です。
そのため最後まで正確に粘り強く解ける計算力が必要です。
他分野との融合問題が多い
東大数学では複数の分野が組み合わさった問題が出されます。
受験生の知識と理解度を確かめるためです。
例としては、
- 確率と数列の融合問題である「確率漸化式」
- 数列と極限
- 複素数平面と図形の相似
などがあります。
これらの問題に取り組むには、数学全体の幅広い知識を持ちながら、様々な問題に柔軟に対応する能力が求められます。
東大数学の傾向(頻出分野)

KENTEN
過去20年分の過去問を分析してみてわかったことです
文理共通:「周期性」に注意
- 「何度も操作を繰り返すとどうなるのか」という問題が「確率」、「漸化式」、「整数」に多く出題されます。(理系は「微積」や「極限」)
- 文系は「数学的帰納法」の習熟を怠らないようにしたい。
理系は「微分・積分、複素数平面」「空間図形」「多変数関数」を重視
- 理系では数Ⅲの微積が2題出題され、ほかの問題と比べて易しく、「微分・積分」が得点源
- 「複素数平面」も多数出題されており、出題される可能性は高いです。
- 昔から「空間図形」がよく出題されるほか、「多変数関数」の問題も頻出です。
東大数学対策
できる限りすべての問題に手を付け、標準レベルの小問を確実に得点しながら、どの大問を完答することができるかを見極めて解く。
対策まとめ
- 目標:目標点を設定する
- 戦略:暗記数学を進める
- 「計算力」
- 「解法暗記」
- 「試行力養成」
- 戦術:本番までに身に着けるテクニック
- 「問題を見極める力」
- 「論理的で分かりやすい記述答案力」
- 注意点:共通テスト対策も必ず取り組む
①目標:目標点の設定
対策を進めるにあたって最初にするべきことは目標設定と現状把握です。
合格するためには適切に科目ごとに目標点を割り振り、その目標点に到達させるように、学習を計画的に進めていくことが、最善の合格方法です。
ただし、目標は高すぎても低すぎてもいけませんし、個人によって違います。
個人の得意科目・不得意科目、科目ごとの得点の伸ばしやすさの特性を考えた上で、無理のない目標点を設定することが、受験計画のスタートラインです。
特に数学は現時点の実力から現実的に到達可能な点数が絞られてきます。
共通テストで目標を設定する
東大数学の目標設定においては共通テストを実際に解いてみて、その得点から2次試験の目標を設定することをオススメしています。

KENTEN
受験1年前の段階で、共通テスト得点と現実的な目標レベルを示しますので、参考にしてみてください。
| 共通テスト得点 | レベル | 2次目標点 | 完答題 | 部分点題 |
|---|---|---|---|---|
| 110~130 | 文系「守り」 | 25~30点 | 1 | 2 |
| 140~170 | 文系「標準」 | 40~45点 | 2 | 2 |
| 180~200 | 文系「攻め」 | 60~65点 | 3 | 1 |
| 130~150 | 理系「守り」 | 40~45点 | 0~1 | 4~5 |
| 160~180 | 理系「標準」 | 60~70点 | 1~2 | 3~4 |
| 185~200 | 理系「攻め」 | 80~100点 | 3~4 | 2~3 |
目標設定の次は、自分の実力と目標点数とのギャップを理解して、最終目標までの道のりを逆算することが重要です。
自分の実力は、過去問を解いてみれば明らかになります。
多くの方は過去問を解いてもその時点では届かないとは思いますが
- 各科目何点届いていませんでしたか?
- 何をすればその差は埋まりますか?
を徹底的に考え、学習計画を進めていきましょう。
②戦略:暗記数学の進め方
- 複雑な計算を含むことが多いため計算力が必須
- 文理共通戦術として全範囲に渡って標準的な解法パターンをストックし、発展的な解法を特定分野に絞って極めていくこと
- 一方 対称性や置換積分などを用いて計算をうまく簡略化できることもあるので両方からの対策が必須
「暗記数学」は「計算力」、「解法暗記」 、「試行力養成」 の三つの要素 からなります。
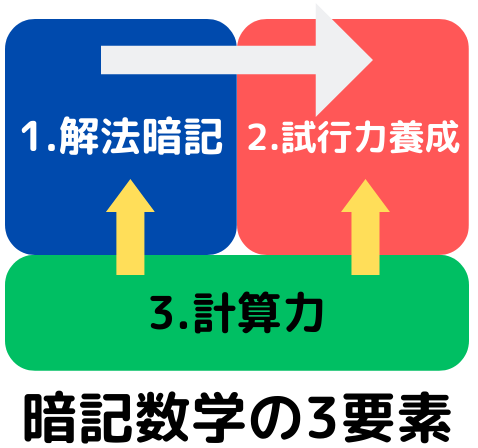
計算力
暗記数学の土台を支えているのが「計算力」です。
「計算力」がないと 解法暗記が効率よく進まず、「試行力養成」でも 計算時間がかかって試行する時間が不足することになってしまいます。
東大数学では、問題は難しくないが計算が複雑な問題がよく出されるので、「計算力」が重要です。
解法暗記
「解法暗記」の段階では基本から標準レベルの解法パターンをストックしていきます。
自力で問題を解きながら解放を身につけるのではなく 5分考えてもわからない問題は模範解答見て覚えるというやり方で解法をストックすると効率よく解法をマスターできます 。
自力で解けるものがあればそのまま解き、時間があれば例題に対応する練習題を解いてみて覚えた解法が適用できるかどうかを試すのがいいでしょう。
回答を見て覚えた例題には印をつけておき翌日、1週間後、1ヵ月後に復習をするようにします。
解法が定着していなければ練習題をやってみてチェックを行います。
試行力養成
「試行力」とはAのやり方でダメだったらBのやり方を試す という頭の働かせ方です。
「解法暗記」で覚えたパターンを「引き出して試す」「組み合わせて試す」といった頭の働かせ方を身につけさせます。
苦手でもなんとか標準問題をクリアできるようにすること第一目標とします。
第二目標はワンランク上の解放ストックで、得意分野を作ることに力を注ぎます。
数学が得意な人でもさすがに難レベルの問題になると本番で確実に取れる保証はどこにもないので、標準問題の解法パターンの厚みを増やします。
③戦術:本番までに身に着けたいこと
- 難問か標準問題かを見極める力
- 論理的で分かりやすい記述答案を書くこと
難問と標準問題を見極める力
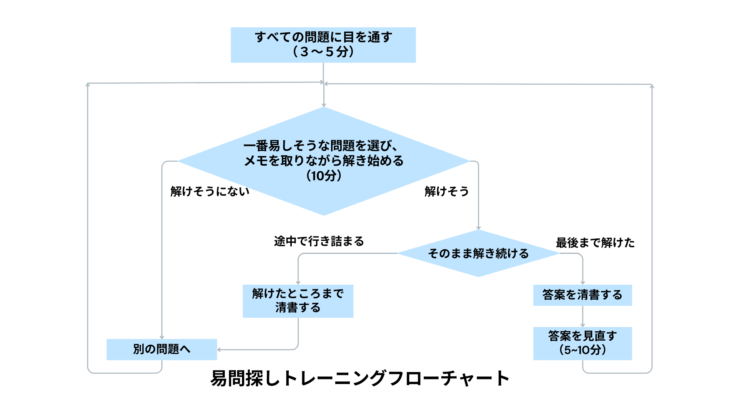
- すべての問題に目を通す (3~5分 )
- 一番易しそうなものを選びメモを取りながら解きはじめる 。(10分)
- 解けそうならそのまま続け、解けそうになければ別の問題へ。
- 最後まで解けたら答案を清書し答案を見直す (5~10分)
- 途中で行き詰ったら解けたところまで清書する
- 残りの問題の中から一番得意そうな問題を選びメモを取りながら解きはじめる (10分)≪2~6繰り返し≫
文系は100分で4題、理系は150分で6題出題されるので、どれが難問でどれが標準問題かのあたりをつけ、解ける問題から手を付けることが重要です。
フローチャートのように解けるよう練習しましょう。
トレーニングには東大の過去問や模試問題集などを利用します。
論理的で分かりやすい記述答案力
問題は最後までとききれなかったときでも自分が到達できたところまででいいから言葉でまとめておくことが大切な答案戦術です。
説明能力に採点者は一定の評価を与えると言われています。
受験生はよく「完答○点」というようなことを言いますが、最後まで計算が続いていて正答が書いてあるというのと、完全な論理によって正答が表現されている、というのとの間にはかなり大きな差があります。
とは言っても別に重箱の角をつついて減点してやると思っているわけではないので、明確な論理がきちんと書いてあれば、かなりの勘違いや計算ミスがあっても評価できる点は評価します。
そういう答案のほうがいいかげんな理由によってとりあえず正答に達している答案より評価が高くなるということもしばしばありえます。
「東京大学新聞」平成14年9月10日号より
点になる記述答案は東大型模試から学びましょう。
「 東大即応オープン」や「東大入試実戦模試」の解答と解説が良いテキストになります。

KENTEN
自分の答案と模範解答と何がどう違うのかを綿密に分析し、模範解答の真似をするつもりで答案を作るのがオススメ!
解答用紙の使い方
本番の解答用紙はB4版の大きさで文系は表と裏で計4題、理系は計3題。
すなわち一台につき最小でB5版のスペースが与えられます。
このスペースを過不足なく使って点になる答案を書く練習を直前期にやります。
④注意点:共通テスト対策も必ず取り組む
計算力に不安があれば計算力トレーニングをしておきましょう 。
センターの過去問や模試問題集を計算ドリルに見立てて集中的にやっておくといいでしょう 。
東大数学オススメ参考書ルート
文系理系レベル別にオススメの参考書ルートを紹介します。
自分の目標別に該当箇所を選んでください。
文系「守り」レベル(目標:30点)
- STEP
解法暗記
- STEP
試行力養成
- 難関大 文系・理系数学(マセマ)1ヶ月
- 文系数学 入試の核心(Z会) 1ヶ月
文系数学・入試の核心は100問と問題数が多いのでまずは奇数題だけ解くなどし、時間次第でさらに解いて補強するのがよいでしょう。
- STEP
実戦演習
- 試行力養成の残り
- 過去問
- 模試問題集
文系「標準」レベル(目標:45点)
- STEP
解法暗記
- STEP
試行力養成
- 文系数学の良問プラチカ(河合出版)1.5~2ヶ月
- 難関大 文系・理系数学(マセマ)1ヶ月
解法暗記では狙い撃ちをしましたが、文系プラチカを使って全範囲まんべんなく演習します。
第2段階の試行力養成としては難関大文系・理系数学を使います。
- STEP
実戦演習
- 試行力養成の残り
- 過去問
- 模試問題集
文系「攻め」レベル(目標:65点)
- STEP
解法暗記
- STEP
試行力養成
- 文系数学の良問プラチカ(河合出版)1.5~2ヶ月
- 新数学スタンダード演習(東京出版)2か月
文系プラチカは解答が充実しており、別解があれば丁寧に理解しておきたい。
Ⅰつの問題に対する複数の解法を理解しておくことで、標準レベルより上の問題への対応力が身につきます。
時間的にも問題レベル的にも余力があれば、スタ演ⅠⅡAB へ。
200問以上あるので、2ヶ月は確保したいです。
- STEP
実戦演習
- 試行力養成の残り
- 過去問
- 模試問題集
理系「守り」レベル(目標:45点)
- STEP
解法暗記
- STEP
試行力養成
- 理系数学・入試の核心・標準編(Z会出版)2ヶ月
- チョイス新標準問題集数学Ⅲ(微分・積分のみ)(河合出版)1週間
核心標準は入試標準レベルの問題を数多く掲載しており、文理共通問題はこのⅠ冊でカバーできます。
チョイス新標準問題集は問題数が多いので、微分・積分の問題に絞ります。
- STEP
実戦演習
- 試行力養成の残り
- 過去問
- 模試問題集
理系「標準」レベル(目標:70点)
- STEP
解法暗記
- STEP
試行力養成
- 理系数学・入試の核心・標準編(Z会出版)2ヶ月
- やさしい理系数学(河合出版)(河合出版)1ヶ月
2冊とも全問解けば東大の文理共通問題とⅢには十分対応できる実力が身につきます。
- STEP
実戦演習
- 試行力養成の残り
- 過去問
- 模試問題集
理系「攻め」レベル(目標:100点)
- STEP
解法暗記
- 新数学スタンダード演習ⅠⅡAB(東京出版)2か月
- 数学Ⅲスタンダード演習(東京出版)2ヶ月
東大2次で必要とされる解法にしぼり解法暗記を進めます。
- STEP
試行力養成
- STEP
実戦演習
- 試行力養成の残り
- 過去問
- 模試問題集
東大数学オススメ参考書解説
数学の問題集を使いこなすために問題集の特色をつかんでおきましょう。
チャート式基礎からの数学(青チャート)(数研出版)
網羅性と解法のオーソドックスさから、中堅大学~難関大学全般におすすめ。
時間的に余裕のある1~2年生は青チャートで解法暗記を終えてから後述の「1対1演習」シリーズにいった方が接続がスムーズで学校の授業との連携もよくてオススメ 。
大学への数学 一対一対応の演習数学シリーズ(東京出版)
- 少ない問題数で標準問題への対応力をつけられます。
- 標準的な解法がすでに身に付けられていることが使用条件です。
一つの例題と一つの演習題がセットになっています。
1冊あたり70~90例題。一日に3~4題のペースで進められれば1ヶ月で終えられます。
チャート式シリーズ入試必携168文系対策数学12AB(数研出版)
数学が得意でない人には文理問わず薦めたいです。
レベルとしては 上限は青チャートよりやや下で下限は黃チャートよりも上です 。
基本的に例題のみをとき進めればOK。しっくりこなければ類題も解いてみます。
大学への数学・新数学スタンダード演習 、大学への数学・数学Ⅲスタンダード演習(東京出版)
最高レベルの解法を習得するために使います。
1対1演習をⅠⅡABとⅢに分け、発展的な問題まで掲載した参考書でさらに難しいです。
難易度はABCDの4段階あるがAとBの問題を確実に定着させることが先決です。
やさしい理系数学 、ハイレベル理系数学(河合出版)
この2冊は理系であればいずれか使いたい良質の問題集で、別解が豊富なので利点です 。
目標点に合わせて選択してください。
典型問題に対して複数の解法を確認することで、問題をヒネられたときにも対応できる可能性が高まります 。
東大数学で一点でも多く取る方法文系編(東京出版)
東大の過去問で最大限に部分点を取るための書き方や答案の書き方を示したユニークな参考書
こういうことを書いても部分点につながるということを知っておくだけでも利点です。
記述式答案の書き方にも取り入れられるところは多いです。
模試問題集
駿台の「東大入試実戦模試」や河合・Z会の「東大即応オープン」の問題を収録した模試問題集。
直前期に実践演習として本番形式で編集を積みながら答案戦術を練り上げていきます。
「東大の文系数学25ヵ年」 、「東大の理系数学25カ年」(数学社)
東大の過去問を分野別に再構成した過去問集。
難易度表示があり解説が詳しいのが特徴。
時間に余裕がある人が苦手分野を集中的に解いたり、標準問題を集中的に解くなど問題集の感覚で使います。
「鉄緑会 東大数学問題集 1981-2020〔40年分〕」(KADOKAWA)
「複素数平面」を含む1981年~2020年の東大入試問題を鉄緑会が徹底的に分析したもの。
値段が高いのですが、質・量ともにトップクラスです。
他の過去問と比較してもかなりの解説量で、別解も豊富に記載されています。
ただ量もかなり多いので取り組む時間が確保できる人むけです。
10年分だけなら他の過去問と問題量が同じなので、直前期でも何とかやりきれるでしょう。
まとめ
東大数学では目標点をとるための基本方針として、確実に解ける標準問題を解き、難問は捨てることが重要です。
そのため、標準問題を完答するための「計算力」、「解法暗記」、「試行力養成」が必要です。

さらにその仕上げとして「易問探しトレーニング」、「記述答案力」を身に着けます。

目標とするレベルに応じて、紹介した参考書ルートがオススメです。
実際に勉強計画を立てるときの注意点を次の章で解説します。
絶対に東大に合格したい人へ

KENTEN
ここまで東大数学の一般的な攻略法を説明しましたが、一人ひとりに合った目標設定や計画をたてないとダメです。
なぜなら自分では正しいと思っていても、実は間違った目標を設定をしてしまい失敗するケースは多いから。
参考書ルートなどできるだけ細かく説明したつもりですが、授業進度、学習状況、目標点、受験までの残り時間が違うので、計画がひとりひとり全く異なるんです。
一番いい解決方法は東大受験のプロからフィードバックを受けること。
東大に合格するにはその道の成功者である東大生に教えてもらうのが一番の近道です。
私がライターを務める東大毎日塾では選び抜かれた東大生メンター(採用率わずか30%以下)が専属で個別指導しています。
ひとりひとりに最適な東大合格のプランを一緒に考えてくれるし、必ずやり遂げられるように徹底的にフォローしてくれます。
完全個別指導で合格に向けた受験戦略を本気で考えますので、まずは無料相談会にお申し込みください!
絶対に東大合格まで導きます!
\14日間無料体験実施中/
40000円キャッシュバック中























